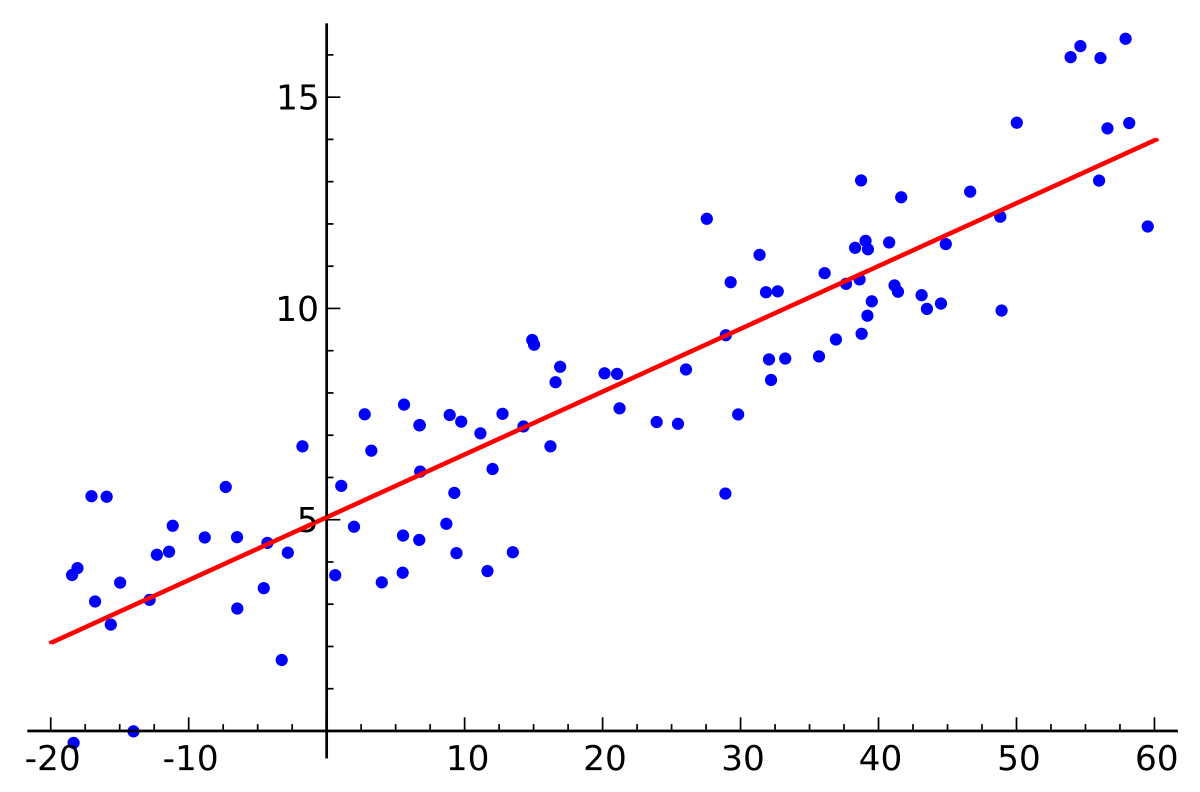
Implementation of various linear regression techniques with visualization and analysis.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.pipeline import Pipeline
# --- 1. Simple Linear Regression ---
def simple_linear_regression_example():
# Generate synthetic data
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1) * 0.5
# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Make predictions
y_pred = model.predict(X_test)
# Print results
print("Simple Linear Regression Results:")
print(f"Coefficient: {model.coef_[0][0]:.4f}")
print(f"Intercept: {model.intercept_[0]:.4f}")
print(f"R² Score: {r2_score(y_test, y_pred):.4f}")
# Visualize results
plt.figure(figsize=(10, 6))
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.scatter(X_test, y_test, color='green', label='Test Data')
plt.plot(X_test, y_pred, color='red', label='Predictions')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Simple Linear Regression')
plt.legend()
plt.grid(True)
# plt.show()
# --- 2. Multiple Linear Regression ---
def multiple_linear_regression_example():
# Generate synthetic data
np.random.seed(42)
X = np.random.rand(100, 3) # 3 features
y = 4 + 2*X[:, 0] + 3*X[:, 1] - 1*X[:, 2] + np.random.randn(100) * 0.5
# Split and scale the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Create and train the model
model = LinearRegression()
model.fit(X_train_scaled, y_train)
# Make predictions
y_pred = model.predict(X_test_scaled)
# Print results
print("
Multiple Linear Regression Results:")
for i, coef in enumerate(model.coef_):
print(f"Coefficient {i+1}: {coef:.4f}")
print(f"Intercept: {model.intercept_:.4f}")
print(f"R² Score: {r2_score(y_test, y_pred):.4f}")
# --- 3. Polynomial Regression ---
def polynomial_regression_example():
# Generate synthetic data with non-linear relationship
np.random.seed(42)
X = np.linspace(-3, 3, 100).reshape(-1, 1)
y = 0.5 * X**2 + X + 2 + np.random.randn(100, 1) * 0.5
# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create polynomial features
degrees = [1, 2, 3] # Try different polynomial degrees
plt.figure(figsize=(15, 5))
for i, degree in enumerate(degrees, 1):
# Create polynomial pipeline
model = Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('linear', LinearRegression())
])
# Fit the model
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# Plot results
plt.subplot(1, 3, i)
plt.scatter(X_train, y_train, color='blue', label='Training Data', alpha=0.5)
plt.scatter(X_test, y_test, color='green', label='Test Data', alpha=0.5)
# Sort X for smooth curve plotting
X_sort = np.sort(X, axis=0)
y_curve = model.predict(X_sort)
plt.plot(X_sort, y_curve, color='red', label=f'Degree {degree}')
plt.xlabel('X')
plt.ylabel('y')
plt.title(f'Polynomial Regression (Degree {degree})')
plt.legend()
plt.grid(True)
plt.tight_layout()
# plt.show()
# --- 4. Regularized Regression ---
def regularized_regression_example():
# Generate synthetic data with many features
np.random.seed(42)
n_samples, n_features = 100, 20
X = np.random.randn(n_samples, n_features)
# True coefficients: only first 5 features are relevant
true_coef = np.zeros(n_features)
true_coef[:5] = [2, -1, 1.5, -0.5, 1]
y = np.dot(X, true_coef) + np.random.randn(n_samples) * 0.1
# Split and scale the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Define models with different regularization
models = {
'Linear': LinearRegression(),
'Ridge': Ridge(alpha=1.0),
'Lasso': Lasso(alpha=1.0),
'ElasticNet': ElasticNet(alpha=1.0, l1_ratio=0.5)
}
# Train and evaluate each model
print("
Regularized Regression Results:")
for name, model in models.items():
model.fit(X_train_scaled, y_train)
y_pred = model.predict(X_test_scaled)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"
{name} Regression:")
print(f"MSE: {mse:.4f}")
print(f"R² Score: {r2:.4f}")
print(f"Number of non-zero coefficients: {np.sum(np.abs(model.coef_) > 1e-10)}")
# Visualize coefficients
plt.figure(figsize=(12, 6))
x = np.arange(n_features)
width = 0.15
for i, (name, model) in enumerate(models.items()):
plt.bar(x + i*width, model.coef_, width, label=name, alpha=0.7)
plt.xlabel('Feature Index')
plt.ylabel('Coefficient Value')
plt.title('Comparison of Coefficients Across Different Regularization Methods')
plt.legend()
plt.grid(True)
# plt.show()
# --- Main Execution ---
if __name__ == "__main__":
print("Running Linear Regression Examples...")
# Run all examples
simple_linear_regression_example()
multiple_linear_regression_example()
polynomial_regression_example()
regularized_regression_example()